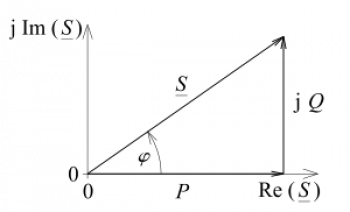
Das Leistungsdreieck, auch als Watt-Dreieck bekannt, ist eine grafische Darstellung, die in der Elektrotechnik zur Analyse der Leistungsverteilung in einem Wechselstromkreis verwendet wird.
Es basiert auf den trigonometrischen Eigenschaften eines rechtwinkligen Dreiecks, wodurch wir die Beziehung zwischen den drei Grundkräften eines elektrischen Systems berechnen und verstehen können:
- Scheinleistung (\( S \)) : Stellt die dem Stromkreis zugeführte Gesamtleistung dar und wird in Voltampere (VA) gemessen. Es handelt sich um die Vektorkombination aus Wirk- und Blindleistung.
- Wirkleistung (\( P \)) : Dies ist die Nutzleistung, die in tatsächliche Arbeit umgewandelt wird, wie beispielsweise Beleuchtung oder die Bewegung von Motoren. Die Messung erfolgt in Watt (W).
- Blindleistung (\( Q \)) : Dies ist die Leistung, die keine Nutzarbeit verrichtet, aber für den Betrieb von Geräten mit induktiven Elementen (wie Transformatoren und Motoren) erforderlich ist. Die Messung erfolgt in Blindvoltampere (VAR).
Formel des Potenzdreiecks
Das Dreieck besteht aus drei Seiten, wobei:
- Die Hypothenuse stellt die Scheinleistung (\( S \)) dar.
- Der angrenzende Schenkel ist die Wirkleistung (\( P \)), bezogen auf den Kosinus des Phasenwinkels (\( \cos\theta \)).
- Die Gegenachse ist die Blindleistung (\( Q \)), bezogen auf den Sinus des Phasenwinkels (\(\sin\theta \)).
- Mathematisch wird die Beziehung zwischen diesen Potenzen durch den Satz des Pythagoras ausgedrückt:
\[ S^2 = P^2 + Q^2 \]
Der Leistungsfaktor (PF) ist definiert als das Verhältnis von Wirkleistung zu Scheinleistung:
\[ FP = \cos\theta = \frac{P}{S} \]
Ein niedriger Leistungsfaktor bedeutet einen hohen Blindleistungsanteil, der die Effizienz des elektrischen Systems verringert.
Praktische Beispiele zum Machtdreieck
Nachfolgend zeigen wir drei Praxisbeispiele
Elektromotor mit niedrigem Leistungsfaktor
Ein Induktionsmotor verbraucht 10 kW Wirkleistung und hat aufgrund seiner induktiven Natur eine Blindleistung von 6 kVAR.
Die Scheinleistung beträgt:
\[ S = \sqrt{(10^2 + 6^2)} = \sqrt{100 + 36} = \sqrt{136} \approx 11,66 \text{ kVA} \]
Beleuchtungssystem mit Leistungsfaktorkorrektur
Ein Satz LED-Lampen verbraucht 5 kW bei einer Blindleistung von 1 kVAR.
Die Scheinleistung beträgt:
\[ S = \sqrt{(5^2 + 1^2)} = \sqrt{25 + 1} = \sqrt{26} \approx 5,1 \text{ kVA} \]
Transformator mit induktiver Last
Ein Transformator liefert 50 kW an ein System mit einer induktiven Last, die 30 kVAR benötigt.
Die Scheinleistung des Systems beträgt:
\[ S = \sqrt{(50^2 + 30^2)} = \sqrt{2500 + 900} = \sqrt{3400} \approx 58,3 \text{ kVA} \]
Wofür wird das Potenzdreieck verwendet?
Das Leistungsdreieck ist ein grundlegendes Werkzeug bei der Analyse und dem Entwurf elektrischer Systeme. Zu seinen Anwendungen gehören:
Berechnung der elektrischen Leistung
Damit lässt sich die Leistungsverteilung in einem Stromkreis bestimmen:
- Die gesamte gelieferte Scheinleistung (S).
- Wirkleistung (P), die in Nutzenergie umgewandelt wird.
- Blindleistung (Q), die die zwischen induktiven und kapazitiven Komponenten ausgetauschte Energie darstellt.
Optimierung der Schaltungsleistung
Durch das Verständnis der Energieverteilung können Energieverluste minimiert und der Leistungsfaktor verbessert werden, wodurch unnötiger Blindleistungsverbrauch reduziert und die Nutzung des Stromnetzes optimiert wird.
Entwurf elektrischer Systeme
Es wird zur Dimensionierung elektrischer Geräte verwendet und stellt sicher, dass Transformatoren, Generatoren und Kabel für die erforderliche Leistung geeignet sind, ohne dass es zu Überlastungen oder übermäßigen Verlusten kommt.
Leistungsfaktorkorrektur
Viele industrielle elektrische Systeme erfordern Kondensatorbatterien, um Blindleistung auszugleichen und den Leistungsfaktor zu verbessern. Dadurch wird der Energiebedarf aus dem Netz reduziert und die Betriebskosten gesenkt.
Fehleranalyse und vorbeugende Wartung
Das Leistungsdreieck ermöglicht die Erkennung von Problemen in elektrischen Systemen, wie beispielsweise Energieverlusten aufgrund hoher Reaktanz oder Lastungleichgewichten, und trägt so dazu bei, Ausfälle zu vermeiden und die Wartung zu optimieren.
Gelöste Übung zum Potenzdreieck
Stellungnahme:
Es handelt sich um einen Stromkreis mit einer Scheinleistung von 800 VA und einem Leistungsfaktor von 0,8. Berechnen Sie die Wirkleistung und Blindleistung des Stromkreises.
Lösung:
Zunächst können wir die Wirkleistung (P) des Stromkreises mit der Formel P = S x cos(θ) berechnen, wobei θ der Phasenwinkel zwischen Strom und Spannung ist. Da in diesem Fall der Leistungsfaktor (PF) 0,8 beträgt, wissen wir, dass cos(θ) = PF = 0,8. Daher können wir die Wirkleistung wie folgt berechnen:
\[
P = 800 \, VA \times 0,8 = 640 \, W
\]
Die Wirkleistung der Schaltung beträgt 640 Watt.
Dann können wir die Blindleistung (Q) des Stromkreises mit der Formel Q = S x sin(θ) berechnen. Wir wissen, dass der Phasenwinkel (θ) aus dem Leistungsfaktor mithilfe der folgenden Formel berechnet werden kann:
\[
\cos(\theta) = \text{FP} \quad \Rightarrow \quad \sin(\theta) = \sqrt{1 - \cos^2(\theta)}
\]
Da in diesem Fall FP = 0,8 ist, können wir sin(θ) wie folgt berechnen:
\[
\sin(\theta) = \sqrt{1 - 0,8^2} = \sqrt{1 - 0,64} = \sqrt{0,36} = 0,6
\]
Daher können wir die Blindleistung wie folgt berechnen:
\[
Q = 800 \, VA \times 0,6 = 480 \, VAR
\]
Die Blindleistung des Stromkreises beträgt 480 Voltampere.
Daher beträgt die Wirkleistung des Stromkreises 640 W und die Blindleistung 480 VAR.