Das Dreieck ist ein Polygon, das aus drei geschlossenen Segmenten besteht, die drei verschiedene Punkte (Eckpunkte) verbinden. Die Eckpunkte eines Dreiecks können nicht kollinear sein. Diese geometrische Figur ist eine der grundlegenden polygonalen Formen der Geometrie.
Das Dreieck ist eine der wichtigsten und am weitesten verbreiteten geometrischen Figuren in Wissenschaft und Technik, weshalb die Untersuchung seiner Eigenschaften seit der Antike durchgeführt wird. Ein offensichtliches Beispiel haben wir in den Pyramiden von Ägypten.
Eine wichtige Eigenschaft von Dreiecken ist, dass sie nicht verformt werden können. Aus diesem Grund werden sie häufig bei der Gestaltung von Strukturelementen in der Architektur (das Design des Eiffelturms basiert auf einer Komposition dreieckiger Formen) und im Ingenieurwesen (z. B. feste Stützen für Sonnenkollektoren) verwendet.
In der Geometrie ist es von großer Bedeutung, weil alle Polygone in Dreiecke zerlegt werden können.
Arten von Dreiecken
Diese geometrischen Figuren lassen sich nach verschiedenen Kriterien klassifizieren:
Durch die Größe der Innenwinkel kann es sein:
Spitzes Dreieck: Alle Innenwinkel sind spitz (weniger als 90 Grad).
Stumpfes Dreieck: Es gibt einen Winkel, der größer als 90 Grad ist.
Rechtwinkliges Dreieck: einer der Winkel ist 90 Grad, ein rechter Winkel. In diesem Fall werden die beiden Seiten, die einen rechten Winkel bilden, Beine genannt, und die Seite, die dem rechten Winkel gegenüberliegt, wird Hypotenuse genannt.
Wie in der euklidischen Geometrie beträgt die Summe der Winkel eines Dreiecks 180º. Daher müssen mindestens zwei Winkel im Dreieck spitz sein (weniger als 90º).
Durch die Anzahl gleicher Seiten können diese Figuren sein:
Ungleichmäßiges Dreieck: Alle drei Seiten sind nicht gleich.
Gleichschenkliges Dreieck: Zwei Seiten sind gleich. Diese Seiten heißen Seite, die dritte Seite heißt Basis. In einem gleichschenkligen Dreieck sind die Basiswinkel gleich.
Gleichseitiges Dreieck: Alle drei Seiten sind gleich. In einem gleichseitigen Dreieck sind alle Winkel gleich 60°.
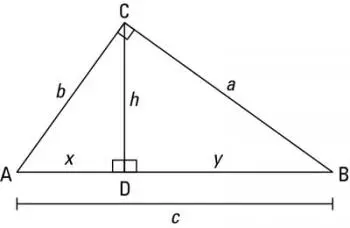
Wie berechnet man die Fläche und den Umfang eines Dreiecks?
Basierend auf der folgenden Abbildung können wir die folgenden Formeln verwenden, um den Umfang und die Fläche eines Dreiecks zu erhalten:
Um den Umfang zu berechnen, müssen wir einfach die Seitenlängen der Figur addieren: a + b + c.
Die Formel, um die Fläche eines Dreiecks zu finden, ist das halbe Produkt der Grundfläche (nicht der Seiten) mal der Höhe:
A = (b h) / 2
Falls wir die Höhe nicht kennen, können wir die Formel von Heron anwenden.
Woher:
a, b und c entsprechen den drei Seiten der geometrischen Figur.
A ist die Fläche
s ist der Halbumfang (ermitteln Sie den Umfang und teilen Sie ihn durch zwei):
Bei einem rechtwinkligen Dreieck ist eines der Beine die Basis und das andere entspricht der Höhe. Dies erleichtert die Berechnung der Fläche.
