Geometrie ist ein Zweig der Mathematik, der sich auf die Untersuchung der Formen, Größen und Eigenschaften geometrischer Objekte wie Punkte, Linien, Segmente, Polygone und Kreise konzentriert.
Eines der grundlegenden Themen in der Geometrie und insbesondere in Dreiecken ist das Studium von Winkeln und Segmenten, und einer der wichtigsten Sätze im Zusammenhang mit diesen Konzepten ist der Winkelhalbierendesatz.
Dieser Satz spielt eine entscheidende Rolle bei der Aufteilung von Winkeln und Segmenten und findet Anwendung in verschiedenen Bereichen der Mathematik und Physik.
Definition von Winkeln und Winkelhalbierenden
Bevor wir uns mit dem Winkelhalbierendensatz befassen, ist es wichtig, einige Schlüsselkonzepte der Geometrie zu verstehen. Ein Winkel ist der Bereich, der von zwei Strahlen gebildet wird, die einen gemeinsamen Punkt haben, der Scheitelpunkt genannt wird. Winkel werden in Grad gemessen und ein Vollwinkel beträgt 360 Grad. In vielen Fällen müssen wir einen Winkel in zwei gleiche Teile teilen, und das führt uns zum Begriff einer Winkelhalbierenden.
Eine Winkelhalbierende ist eine Linie, ein Strahl oder eine Strecke, die den Winkel in zwei kongruente Winkel, also zwei Winkel mit demselben Maß, teilt. Mit anderen Worten: Die Winkelhalbierende halbiert den Winkel. Bei einem 90-Grad-Winkel hätte die resultierende Winkelhalbierende auf jeder Seite einen Winkel von 45 Grad.
Der Dreieckshalbierendesatz
Der Winkelhalbierendesatz besagt, dass in einem Dreieck die Winkelhalbierende die gegenüberliegende Seite in Segmente teilt, die proportional zu den beiden anderen Seiten sind. Dies mag wie eine komplexe Aussage erscheinen, aber wir können sie anhand eines Beispiels aufschlüsseln und besser verstehen.
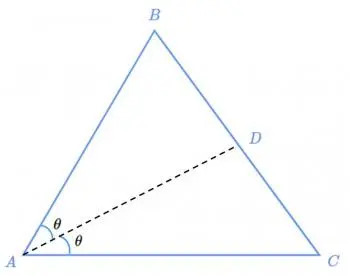
Stellen Sie sich ein Dreieck ABC vor, bei dem der Winkel am Scheitelpunkt A durch eine Linie halbiert wird, die die gegenüberliegende Seite BC am Punkt D kreuzt. Der Satz sagt uns, dass das Verhältnis zwischen BD und CD gleich dem Verhältnis zwischen AB und AC ist.
Mathematisch lässt sich dies wie folgt ausdrücken:
Dieser Satz ist besonders nützlich bei der Lösung von Geometrieproblemen mit Winkeln und Segmenten. Es kann uns helfen, unbekannte Längen zu finden oder Eigenschaften von Dreiecken und anderen geometrischen Figuren zu demonstrieren.
Beweis des Winkelhalbierendensatzes
Der Beweis des Winkelhalbierenden-Theorems beinhaltet die Verwendung von Eigenschaften ähnlicher Dreiecke und die Anwendung des Satzes von Thales. Hier ist eine kurze Erklärung, wie es demonstriert wird:
-
Wir beginnen mit dem Dreieck ABC und seiner Winkelhalbierenden, die die Seite BC im Punkt D schneidet.
-
Wir wenden den Satz von Thales an, der besagt, dass proportionale Segmente entstehen, wenn wir zwei parallele Linien haben, die durch Querlinien geschnitten werden. In diesem Fall zeichnen wir eine Linie parallel zu den Seiten AC und BD, die durch Punkt C verläuft.
-
Dies ergibt zwei ähnliche Dreiecke: ACD und ABC, bei denen die Winkel gleich und die Linien parallel sind, was proportionale Segmente impliziert.
-
Mithilfe der Ähnlichkeitseigenschaft von Dreiecken können wir Folgendes feststellen:
Dies ist die Gleichheit, die wir beweisen wollten, und damit ist der Beweis des Satzes abgeschlossen.
Beispiele für Anwendungen des Satzes
Der Winkelhalbierendesatz hat mehrere Anwendungen in der Geometrie und Mathematik. Zu den häufigsten Anwendungsbeispielen gehören:
- Lösung von Geometrieproblemen: Der Satz wird verwendet, um unbekannte Längen oder Winkel in Dreiecken und anderen geometrischen Figuren zu finden, wenn bestimmte Proportionsbeziehungen bekannt sind.
- Demonstration der Eigenschaften von Dreiecken: Wird verwendet, um zu zeigen, dass bestimmte Dreiecke ähnlich sind oder dass bestimmte Punkte auf einer geraden Linie liegen.
- Geometrische Konstruktion: Hilft bei der Konstruktion genau halbierter Winkel, was bei verschiedenen Design- und Architekturanwendungen nützlich ist.
- Trigonometriestudien: Der Satz wird auch in der Trigonometrie angewendet, um Probleme im Zusammenhang mit Sinus, Cosinus und Tangens zu lösen.
- Physikalische Problemlösung: Wird in der Physik verwendet, um die Flugbahnen von Teilchen und die Richtung von Kräften in physikalischen Systemen zu verstehen.
