
Ein Quadrat ist eine regelmäßige geometrische Form mit vier gleichen Seiten und vier rechten Winkeln (90 Grad) zwischen diesen Seiten.
Ein Quadrat kann als regelmäßiges Polygon, ebenes und konvexes Viereck klassifiziert werden. Diese ebene Figur ist ein Sonderfall des Rechtecks, der Raute, des Parallelogramms, des Trapezes und des Drachens.
Um diese Form zu rekonstruieren, müssen wir nur die Seitenlänge oder die Diagonale kennen.
Quadrate kommen in vielen geometrischen Körpern vor, aber ein besonderer Fall ist ein Würfel. Ein Würfel ist ein platonischer Körper, dessen Flächen (sechs) aus Quadraten bestehen. Der Würfel ist der einzige platonische Körper mit quadratischen Flächen.
Das Quadrat ist auch die Grundform eines platonischen Mosaiks.
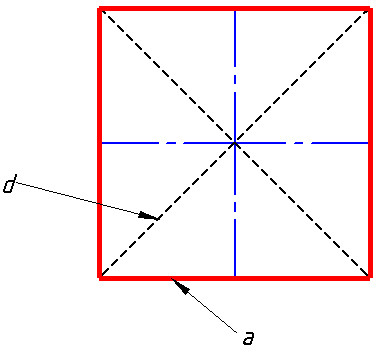
Welche Eigenschaften hat ein Quadrat?
-
Alle vier Seiten sind gleich lang. Es ist also eine Raute und ein gleichseitiges Vieleck.
-
Die vier Innenwinkel sind gleich, also ist es ein Rechteck und ein gleichwinkliges Vieleck. Daher sind Innenwinkel rechte Winkel (90º messen).
-
Die beiden Diagonalen des Quadrats sind gleich, halbieren sich gegenseitig und sind orthogonal.
-
Die Begrenzung eines Quadrats ist viermal so lang wie eine Kante.
-
Der Schnittpunkt der Diagonalen ist der Mittelpunkt, Umkreismittelpunkt und Inkreismittelpunkt und das Symmetriezentrum. Das Quadrat ist sowohl eine Sehnen- als auch eine Vierecktangente.
-
Die Fläche des Umkreises ist doppelt so groß wie die Fläche des Inkreises.
-
Es hat vier Symmetrieachsen: die beiden Mittelsenkrechten und die Diagonalen.
-
Es ist vierfach rotationssymmetrisch und damit auch punktsymmetrisch.
-
Die Symmetriegruppe ist die Diedergruppe D4.
In der euklidischen Geometrie ist das Quadrat der besondere zweidimensionale Fall des Hyperwürfels und des Kreuzpolytops.
Der Begriff eines Quadrats wird in der synthetischen Geometrie der affinen Ebene verallgemeinert, indem eine der äquivalenten Aussagen verwendet wird, die ein Quadrat in der elementaren Geometrie beschreiben, um die Idee zu definieren. Bei voreuklidischen Plänen wird die Existenz dieser Figuren beispielsweise zu einer zusätzlichen Hypothese.
In nichteuklidischen Geometrien sind Quadrate im Allgemeinen Polygone mit vier gleichen Seiten und gleichen Innenwinkeln.
Ein Quadrat ist ein Polygon in Kugelgeometrie, dessen Seiten Großkreise sind, die sich unter demselben Winkel schneiden. Im Gegensatz zu Quadraten mit planarer Geometrie sind die Winkel eines sphärischen Quadrats wichtiger als ein rechter Winkel. Daher haben größere sphärische Quadrate größere Winkel.
Quadrate mit rechten Winkeln gibt es in der hyperbolischen Geometrie nicht. Stattdessen haben Quadrate Winkel, die kleiner als ein rechter Winkel sind. Größere hyperbolische Quadrate haben kleinere Winkel.
Satz des Pythagoras
Um die Seitenlänge zu ermitteln, können wir den Satz von Pitagora verwenden.
Das müssen wir nach dem Satz des Pythagoras wissen:
-
Die Hypotenuse eines rechtwinkligen Dreiecks ist gleich der Quadratwurzel aus der Summe der Quadrate der Schenkel.
-
Der Schenkel eines rechtwinkligen Dreiecks ist gleich der Quadratwurzel der Hypotenuse zum Quadrat minus dem anderen Schenkel zum Quadrat.
Nach seiner Formel:
d2 = a2 + a2 _
Also a = √(d 2 / 2)
Formel zur Berechnung der Fläche eines Quadrats
Um die Fläche zu finden, können wir die folgende Formel verwenden:
wo
-
A ist die Form der Gesamtfläche.
-
a ist die Länge einer Seite (sie sind alle gleich)
-
d ist die Länge der Diagonalen des Quadrats von einem Eckpunkt zum gegenüberliegenden Eckpunkt.
Wie berechnet man den Umfang eines Quadrats?
Das Quadrat des Umfangs ist die Gesamtlänge seiner Seiten, die Länge der Grenze. Dies ist die Formel, um den Umfang der Form zu finden:
P = 4 a
wo,
-
P ist der Umfang der geometrischen Figur
-
a ist die Länge einer Seite des Quadrats.
Welche anderen geometrischen Figuren können ein Quadrat sein?
Das Quadrat kann auch innerhalb anderer geometrischer Figuren definiert werden, wenn sie einige Bedingungen erfüllen:
-
Ein Rechteck mit zwei benachbarten Seiten gleicher Länge.
-
Eine Raute mit zwei benachbarten gleichen Winkeln.
-
Eine Raute mit einem rechten Winkel.
-
Ein Parallelogramm mit zwei gleichen benachbarten Seiten und zwei gleichen benachbarten Winkeln.
-
Ein Parallelogramm mit zwei benachbarten gleichen Seiten und einem rechten Winkel.
-
Ein Viereck mit orthogonalen Diagonalen gleicher Länge, die sich halbieren.
Was bedeutet die Quadratur des Kreises?
Die Quadratur des Kreises ist ein klassisches Problem in der Geometrie. Die Aufgabe besteht darin, aus einem gegebenen Kreis in endlich vielen Schritten ein flächengleiches Quadrat zu konstruieren. Sie ist gleichbedeutend mit der sogenannten Kreisgleichrichtung, also der Konstruktion einer Geraden, die dem Umfang eines Kreises entspricht.
Was ist das magische Quadrat?
Ein magisches Quadrat der Kantenlänge n ist eine quadratische Anordnung der natürlichen Zahlen 1, 2, ..., n², bei der die Summen der Zahlen in allen Zeilen, Spalten und den beiden Diagonalen gleich sind. Diese Summe wird die magische Quadratzahl genannt.
