Ein Kreis ist eine ebene geometrische Form, deren Punkte von einem bestimmten Punkt auf dieser Ebene (dem Mittelpunkt) gleich weit entfernt sind. Der Abstand der Umfangspunkte zum Mittelpunkt ist der Radius oder Radius. Das Wort Kreis leitet sich von einem griechischen Wort ab, das „Reif ODER Ring“ bedeutet.
Verwechseln Sie niemals einen Kreis mit einem Vieleck. Es ist kein Polygon, weil es aus Kurven besteht.
Die Geschichte dieser Form ist uralt. Früher glaubten die Menschen, dass der Mond, die Sonne und andere Planeten kreisförmig seien, weil es kein Konzept für dreidimensionale Formen gab; Mathematiker studierten Kreise, die ihnen halfen, Analysis und Astronomie zu entwickeln.
Kongruente Kreise haben denselben Radius, unabhängig davon, wo ihr Mittelpunkt liegt.
Was ist der Unterschied zwischen einem Kreis und einem Umfang?
Ein Kreis ist eine ebene Fläche, die von einer Reihe von Punkten in Form einer Kurve begrenzt wird.
Auf der anderen Seite ist ein Umfang eine kontinuierliche gekrümmte Linie. Daher ist der Umfang eines Kreises ein Umfang. Da der Umfang eine Linie und keine ebene Fläche ist, hat er keine Fläche, aber einen Umfang.
Der Unterschied zwischen beiden besteht darin, dass der Kreis die gesamte Fläche ist, die innerhalb des Umfangs enthalten ist, während der Umfang der äußere Rand des Kreises ist.
Was sind die Teile eines Kreises?
Es gibt mehrere einzelne Punkte, Linien und Segmente auf dem Umfang:
-
Zentrum: Es ist der innere Fixpunkt, der von allen Punkten auf dem Umfang gleich weit entfernt ist.
-
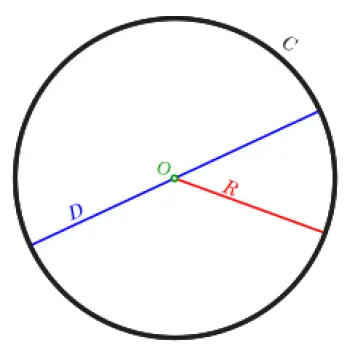
Durchmesser: Es ist die gerade Linie, die zwei gegenüberliegende Punkte des Umfangs verbindet und durch ihren Mittelpunkt verläuft.
-
Radius: Segment, das die Mitte mit einem Punkt am Umfang verbindet.
-
Sehne: Die Sehne eines Kreises erhält man, indem man eine gerade Linie zeichnet, die zwei Punkte auf dem Umfang verbindet. Die Sehne teilt die Form in das Moll-Segment – das die kleinste Fläche hat – und das Dur-Segment.
-
Sekantenlinie: diejenige, die den Umfang in zwei Punkten schneidet.
-
Tangente: die Linie, die den Umfang an einem einzigen Punkt berührt.
-
Tangentenpunkt: der Berührungspunkt der Tangente mit dem Umfang.
-
Arc: Es ist ein Segment des Kreises. Somit gehören alle Punkte zu seinem Umfang.
-
Halbkreis: ist ein Kreissektor, der dem halben Umfang entspricht. Die Enden eines Durchmessers begrenzen einen Halbkreis.
Wie findet man die Fläche eines Kreises?
Die Formel zur Berechnung der durch einen Umfang begrenzten Fläche lautet:
A = π · r2
Woher,
-
π ist die Zahl Pi , eine mathematische Konstante, die ungefähr 3,1416 beträgt.
-
„r“ ist der Radius, dessen Einheit im internationalen Maßsystem Meter (m) ist, obwohl andere Längenmaße verwendet werden können.
-
„A“ ist die Gesamtfläche. Wenn die Formel mit dem Radius in Metern berechnet wurde, sind die Einheiten der Fläche Quadratmeter (m²). Wir können die Fläche jedoch auch in anderen Quadrateinheiten wie Quadratzoll oder Quadratfuß definieren.
Wie finde ich den Umfang eines Kreises?
Die Formel für den Umfang lautet:
P = 2 · π · r
Woher
-
P ist der Umfang.
-
π ist die Konstante Pi, die gleich 3,146 ist.
-
r ist der Radius des Kreises.
Wie findet man den Durchmesser eines Kreises?
Wir können den Durchmesser des Kreises mit der Formel definieren, um den Umfang oder die Fläche zu finden, je nachdem, ob wir den Wert des Umfangs oder der Fläche kennen.
Dazu müssen wir nur berücksichtigen, dass der Durchmesser (d) doppelt so groß ist wie der Radius (r). Daher können wir in den obigen Formeln (r) durch (d/2) ersetzen.
Die beiden Formeln zum Ermitteln des Durchmessers lauten:
-
Wenn wir die Fläche (A) kennen: d = 2 √(A/π), die Quadratwurzel der Fläche dividiert durch Pi und multipliziert mit 2.
-
Wenn wir den Umfang (P) kennen: d = P / π
-
Wenn wir den Radius (r) des Umfangs kennen: d = r · 2