Der Satz von Gauß für das elektrische Feld besagt, dass der Fluss eines elektrischen Feldes durch eine geschlossene Oberfläche (Gaußsche Oberfläche) durch den Quotienten zwischen der gesamten elektrischen Ladung innerhalb der Oberfläche geteilt durch die absolute Dielektrizitätskonstante des Mediums (ε 0 ) gegeben ist. Eine externe Punktlast auf die Oberfläche trägt in keiner Weise zur Gesamtströmung bei.
Die Gaußsche Gleichung ist Teil der vier Maxwell-Gleichungen.
Das von zwei statisch geladenen Objekten erzeugte elektrische Feld kann durch zwei äquivalente Verfahren erhalten werden: Anwendung des Coulomb-Gesetzes oder Anwendung des Gauß-Gesetzes. Das Coulomb-Gesetz ist eine einfachere und direktere Art, die elektrische Kraft auszudrücken. Andererseits ist das Gaußsche Gesetz subtiler, eleganter und manchmal nützlicher.
Der Satz von Gauß hat einen sehr praktischen Nutzen. In seiner physikalischen Formulierung in Bezug auf elektrische Felder wird es schließlich in eine einfache Formel übersetzt, die für alle anwendbar ist und sehr bedeutende praktische Implikationen hat.
Der Ladungsfluss, der die Gaußsche Oberfläche durchquert, ist proportional zur Anzahl der Feldlinien, die sie durchqueren.
Aussage des Satzes von Gauß
Hier ist die Aussage des Gaußschen Theorems für das elektrische Feld: Der Fluss eines elektrischen Feldes durch eine geschlossene Oberfläche ist durch das Verhältnis zwischen der gesamten elektrischen Ladung innerhalb der Oberfläche und der absoluten Dielektrizitätskonstante des Mediums gegeben.
Gaußsche Gesetzformel
Wenn wir die Formel des Gaußschen Satzes für das elektrische Feld betrachten, können wir schreiben:
Die Gaußsche Aussage bietet eine schnelle und einfache Möglichkeit, den elektrischen Feldfluss durch eine geschlossene Oberfläche zu berechnen. Berechnen Sie einfach die algebraische Summe aller Ladungen, die sich innerhalb der Oberfläche befinden, und teilen Sie sie durch die absolute Dielektrizitätskonstante.
Es ist wichtig, einige Aspekte hervorzuheben:
-
Wenn wir an das Vakuum denken, können wir die Dielektrizitätskonstante des Vakuums, deren Wert wir kennen, durch die absolute Dielektrizitätskonstante des Mediums ε m ersetzen .
-
Um die algebraische Summe aller internen Ladungen zu berechnen, müssen die Vorzeichen der Ladungen berücksichtigt werden, die positive oder negative Ladungen sein können.
-
Die Oberfläche kann jede beliebige Form haben, solange sie geschlossen ist.
-
Entscheidend ist die Gesamtladung innerhalb der Oberfläche. Liegen andere Lasten außerhalb der Oberfläche vor, sollten diese bei der Strömungsberechnung nicht berücksichtigt werden.
-
Der Satz gilt für jede Art von elektrischem Feld, das nicht unbedingt im Raum gleichförmig ist. Die Formel gilt auch für jede beliebige Lastkonfiguration.
Beispiel für das Gaußsche Gesetz
Angenommen, wir möchten das von einer Punktladung erzeugte elektrische Feld berechnen und verwenden das Gaußsche Gesetz, um es zu finden.
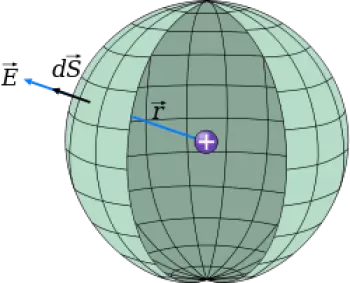
Stellen wir uns in unserem Beispiel eine kugelförmige Gaußsche Fläche vom Radius r vor, in deren Zentrum eine Ladung (q) enthalten ist. Zur Berechnung des Strömungsintegrals nehmen wir an, dass E aufgrund der Symmetrie des Problems die radiale Auswärtsrichtung der Last (q) haben muss. Dies impliziert, dass E an jedem Punkt der Wartefläche parallel zu dS ist.
Auch wegen der Symmetrie müssen wir annehmen, dass E nur vom Abstand r von der Ladung q zum betrachteten Punkt abhängt, so dass E für jeden Punkt auf der Kugel den gleichen Wert hat und bei der Integration konstant ist.
Unter diesen Bedingungen lautet die Berechnung der Strömung durch die Kugeloberfläche:
Φ = E (4 · π · r²)
Da das Integral einfach die Fläche der Kugeloberfläche ist. Da die in unserer Kugel enthaltene Gesamtladung q ist, gibt uns das Gaußsche Gesetz: