Elektrische Schaltkreise sind ein wesentlicher Bestandteil unseres modernen Lebens. Von den einfachsten elektronischen Geräten bis hin zu den komplexesten Stromversorgungssystemen hängt alles vom richtigen Verständnis und der richtigen Analyse der Stromkreise ab.
Im 19. Jahrhundert formulierte der deutsche Physiker Gustav Kirchhoff die Gesetze, die seinen Namen tragen und die zu den grundlegenden Grundlagen der Schaltungsanalyse geworden sind: die Kirchhoffschen Gesetze.
Kirchhoffsches Stromgesetz (Knotengesetz)
Das Kirchhoffsche Stromgesetz, auch als Knotengesetz bekannt, besagt, dass an jedem Knoten eines Stromkreises die algebraische Summe der in diesen Knoten ein- und aus ihm austretenden Ströme gleich Null ist. Mit anderen Worten: Der in einen Knoten hineinfließende Strom ist gleich dem Strom, der aus demselben Knoten herausfließt.
Erläuterung
Ein Knoten ist ein Verbindungspunkt zwischen zwei oder mehr Elementen einer Schaltung. Da sich an einem Knoten (unter stationären Bedingungen) keine elektrische Ladung ansammelt, muss die eingehende Strommenge der ausgehenden Strommenge entsprechen.
Mathematisch wird es wie folgt ausgedrückt:
\[ \sum I = 0 \]
Oder durch Angleichen der Ströme, die in einen Knoten eintreten, an die Ströme, die ihn verlassen:
Wenn wir einen Knoten mit mehreren eingehenden Strömen \( I_1 \),\( I_2 \),\( I_3 \) und mehreren ausgehenden Strömen \( I_4 \), \( I_5 \) betrachten, wobei die eingehenden Ströme als positiv und die ausgehenden Ströme als negativ angenommen werden, lautet die Gleichung wie folgt:
\[ I_1+I_2 + I_3 − I_4−I_5=0 \]
die Umstellung:
\[ I_1+I_2 + I_3 = I_4 + I_5 \]
Dies bedeutet, dass die Summe der eingehenden Ströme gleich der Summe der ausgehenden Ströme ist.
Berechnungsbeispiel
Angenommen, es gibt einen Knoten mit drei Streams:
- \( I_1 = 5A \) Eingabe
- \( I_2 = 3A \) Eintrag
- \( I_3 \) ist ein ausgehender Strom, aber wir kennen seinen Wert nicht.
Wenn wir das geltende Gesetz anwenden, können wir den Wert von \( I_3 \) ermitteln:
\[ I_1 + I_2 = I_3 \]
\[ 5A+3A=I3 \]
\[ I_3=8A \]
Dies zeigt an, dass der den Knoten verlassende Strom 8 Ampere beträgt.
Kirchhoffsches Spannungsgesetz (Maschengesetz)
Die algebraische Summe der Potentialdifferenzen in einem geschlossenen Regelkreis ist gleich Null.
Mathematische Erklärung
Eine Schleife ist jeder geschlossene Pfad innerhalb eines Schaltkreises. Da elektrische Energie in einem Stromkreis weder erzeugt noch vernichtet werden kann, muss die gewonnene Energie (durch Spannungsquellen) der verlorenen Energie (durch Spannungsabfälle an Widerständen und anderen Komponenten) entsprechen.
Mathematisch wird es wie folgt ausgedrückt:
\[ \sum V = 0 \]
Wenn wir in einer Schleife eine Spannungsquelle \( V_1 \) und mehrere Spannungsabfälle \( V_2 \), \( V_3 \), \( V_4 \) haben, lautet die Gleichung wie folgt:
die Umstellung:
Dies bedeutet, dass die Summe der von den Quellen gelieferten Spannungen gleich der Summe der Spannungsabfälle über den Schaltungskomponenten ist.
Zahlenbeispiel
Angenommen, es handelt sich um eine Reihenschaltung mit:
- Eine Batterie mit \( V_1 = 12V \)
- Ein Widerstand mit Spannungsabfall \( V_2 = 5V \)
- Ein weiterer Widerstand mit Spannungsabfall \( V_3 = 7V \)
Anwendung des Spannungsgesetzes:
Dies bestätigt, dass die von der 12-V-Quelle bereitgestellte Leistung auf die beiden Widerstände verteilt wurde.
Anwendung der Kirchhoffschen Gesetze
Die Kirchhoffschen Gesetze sind auf jeden Stromkreis anwendbar, egal ob Gleichstrom (DC) oder Wechselstrom (AC). Diese Gesetze sind besonders nützlich für die Analyse komplexer Schaltkreise, in denen mehrere Strom- und Spannungsquellen sowie eine Vielzahl von Elementen wie Widerstände, Kondensatoren und Induktoren vorhanden sind.
Durch Anwendung der Kirchhoffschen Gesetze ist es möglich, ein Gleichungssystem aufzustellen, mit dessen Hilfe sich die Ströme und Spannungen in den einzelnen Komponenten des Stromkreises bestimmen lassen. Dadurch können wir das Gesamtverhalten des Stromkreises untersuchen und präzise Berechnungen durchführen, um effiziente und zuverlässige Schaltkreise zu entwerfen.
Nachfolgend einige Beispiele für reale Anwendungen:
1. Komplexe Schaltkreise lösen
Mithilfe der Kirchhoffschen Gesetze können wir elektrische Schaltkreise analysieren und lösen, die mehrere Komponenten, Strom- und Spannungsquellen sowie komplexe Verbindungen enthalten. Durch die Anwendung der Kirchhoffschen Gesetze ist es möglich, Gleichungen aufzustellen, die Ströme und Spannungen in jedem Element des Stromkreises in Beziehung setzen, wodurch ihr Verhalten bestimmt und die Strom- und Spannungswerte in verschiedenen Teilen des Stromkreises berechnet werden können.
2. Schaltungen entwerfen und optimieren
Mithilfe der Kirchhoffschen Gesetze können Elektroingenieure Schaltkreise entwerfen und optimieren, um spezifische Anforderungen zu erfüllen. Diese Gesetze vermitteln ein Verständnis für die Verteilung von Strom und Spannung in einem Stromkreis und helfen dabei, kritische Punkte zu erkennen, den erforderlichen Widerstand zu berechnen und einen ordnungsgemäßen Stromfluss sicherzustellen.
3. Analyse elektrischer Netze
Die Kirchhoffschen Gesetze finden auch Anwendung bei der Analyse größerer elektrischer Netzwerke, etwa von Stromverteilungs- oder Übertragungsnetzen. Mithilfe dieser Gesetze lässt sich der Stromfluss in den verschiedenen Zweigen des Netzes bewerten und ausgleichen, mögliche Überlastungsprobleme erkennen und die optimale Konfiguration für eine effiziente Verteilung elektrischer Energie bestimmen.
Beispiele für Kirchhoffs Gesetze
Hier einige Beispiele, die die Anwendung der Kirchhoffschen Gesetze veranschaulichen:
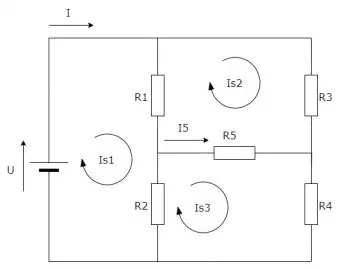
Beispiel 1: Kirchhoffsches Stromgesetz (Knotengesetz)
Angenommen, wir haben einen Schaltkreis mit drei parallel geschalteten Widerständen, die von einer Stromquelle gespeist werden. Wir möchten den Strom in jedem Widerstand bestimmen.
Nach dem Kirchhoffschen Stromgesetz ist die algebraische Summe der in einen Knoten ein- und aus ihm austretenden Ströme gleich Null. In diesem Fall wird der obere Knoten als Referenz verwendet und der Gesamtstrom, der in diesen Knoten eintritt, ist I. Daher können wir die folgende Gleichung aufstellen:
Wobei I1, I2 und I3 die Ströme in jedem Widerstand sind. Durch Lösen dieser Gleichung können die Werte der Ströme in jedem Widerstand ermittelt werden.
Beispiel 2: Kirchhoffsches Spannungsgesetz (Maschengesetz)
Angenommen, wir haben einen Schaltkreis mit drei in Reihe geschalteten Widerständen und einer Spannungsquelle. Wir möchten die Spannung über jedem Widerstand bestimmen.
Gemäß dem Kirchhoffschen Spannungsgesetz ist die algebraische Summe der Potentialunterschiede (Spannungen) in jedem geschlossenen Stromkreis gleich Null. In diesem Fall können wir mithilfe des Maschengesetzes zwei Gleichungen aufstellen:
-
Für die obere Schleife: V = V1 + V2
-
Für die untere Schleife: V = -V2 - V3
Wobei V1, V2 und V3 die Spannungen über jedem Widerstand sind. Durch Lösen dieser Gleichungen können wir die Spannungswerte an jedem Widerstand ermitteln.
Beispiel 3: Kirchhoffsches Spannungsgesetz mit Widerstand
Betrachten Sie eine Schleife mit einer Spannungsquelle und zwei Widerständen:
- \( V_1 = 12V \)
- \(R_1 = 4 \, \Omega \)
- \(R_2 = 2 \, \Omega \)
- \(Ich = 2A \)
Berechnung von Spannungsabfällen
Gesetz der Spannung
\[ 12−8−4=0 \]
Das Kirchhoffsche Spannungsgesetz ist erfüllt.