Im Bereich der Geometrie sind Ebenen Grundelemente. Definiert als unendliche, flache Flächen, die sich in alle Richtungen erstrecken, sind Ebenen grundlegend für das Verständnis von Formen und Strukturen in zwei Dimensionen.
In diesem Artikel werden wir erklären, was Ebenen in der Geometrie sind, welche besonderen Eigenschaften sie haben und wie sie in verschiedenen mathematischen und praktischen Kontexten angewendet werden. Von der Gestaltung geometrischer Figuren bis zur Problemlösung und der Entwicklung technologischer Anwendungen spielen Ebenen eine entscheidende Rolle für unser Verständnis von Raum und Form.
Was ist eine Ebene?
In der Geometrie ist eine Ebene eine unendliche, ebene Fläche, die sich in alle Richtungen erstreckt.
Man kann sie sich vorstellen wie ein Blatt Papier, das sich ewig erstreckt, ohne dick zu sein. In diesem Fall gibt es keine Grenzen oder Kanten, es ist wie eine unendliche Welt in zwei Dimensionen!
Merkmale einer Ebene
Die Hauptmerkmale, die eine Ebene im Raum definieren, sind:
- Unendlichkeit in alle Richtungen: Eines der wichtigsten Merkmale ist, dass sie sich unendlich in alle Richtungen erstreckt. Das bedeutet, dass man immer mehr Platz findet, egal wie weit man sich von einem Punkt auf der Ebene entfernt.
- Keine Dicke: Im Gegensatz zu dreidimensionalen Objekten wie einer Kugel oder einem Würfel hat eine Ebene keine Dicke. Man stelle sich vor, man betrachtet eine Zeichnung auf einem Blatt Papier. Die Zeichnung befindet sich in der Papierebene, aber das Papier ist so dünn, dass es keine Dicke zu haben scheint.
- Dargestellt durch Linien: In der Geometrie stellen wir Ebenen durch Linien dar. Diese Linien können gerade oder gekrümmt sein und erstrecken sich in alle Richtungen innerhalb der Ebene. Wenn wir geometrische Figuren auf einer Ebene zeichnen, verwenden wir diese Linien, um zu zeigen, wie sie zueinander in Beziehung stehen.
- Unabhängig vom Koordinatensystem: Eine Ebene ist unabhängig vom Koordinatensystem, das für ihre Darstellung verwendet wird. Das bedeutet, dass die grundlegenden Eigenschaften der Ebene, wie ihre Unendlichkeit und Dicke, unverändert bleiben, unabhängig davon, wie die x- und y-Achsen gewählt werden.
- Enthält unendlich viele Punkte: Da sie sich unendlich erstreckt, enthält sie unendlich viele Punkte. Jeder Punkt auf der Ebene ist einzigartig und kann durch seine Koordinaten identifiziert werden, wenn ein Koordinatensystem verwendet wird.
- Legt keine bevorzugte Richtung fest: Im Gegensatz zu Linien und Segmenten, die eine bestimmte Richtung haben, hat die Ebene selbst keine bevorzugte Richtung. Man kann sie sich als eine Fläche ohne Orientierung vorstellen, in der alle Richtungen gleichwertig sind.
Arten von Ebenen
In der Geometrie gibt es verschiedene Arten von Ebenen, die für unterschiedliche Zwecke und Anwendungen verwendet werden. Hier sind einige der häufigsten Typen:
- Horizontal: Eine horizontale Ebene erstreckt sich horizontal im Verhältnis zur Erdoberfläche. In einem dreidimensionalen Koordinatensystem ist eine horizontale Ebene nicht geneigt oder vertikal verschoben.
- Vertikal: Im Gegensatz dazu erstreckt sich eine vertikale Ebene senkrecht zur Erdoberfläche. Die Vertikale ist nützlich, um räumliche Beziehungen im dreidimensionalen Raum darzustellen.
- Geneigt: Eine geneigte Ebene ist weder horizontal noch vertikal, sondern bildet einen Winkel mit beiden. Neigungen kommen häufig in physikalischen und mechanischen Problemen vor, wo sie zur Analyse von Kräften, Neigungen und Bewegungen verwendet werden.
- Kartesisch: Ein zweidimensionales Koordinatensystem mit zwei senkrechten Achsen, üblicherweise als x und y bezeichnet. Es wird häufig in der Mathematik verwendet, um Punkte, Graphen und Funktionen darzustellen.
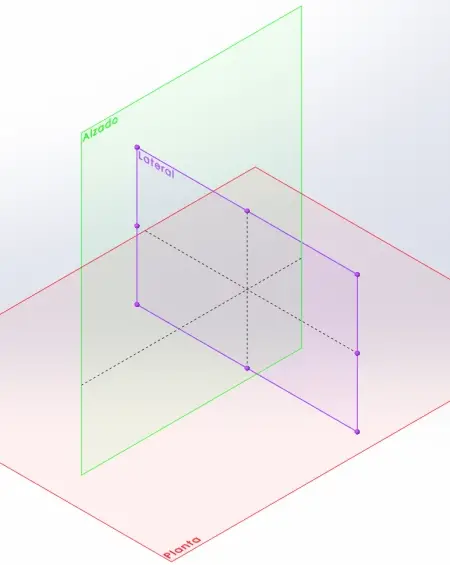
- Projektion: Im technischen Zeichnen und Design wird eine Projektionsebene verwendet, um dreidimensionale Objekte in zwei Dimensionen darzustellen. Projektionspläne umfassen Plan, Aufriss und Seitenansicht, die unterschiedliche Ansichten des Objekts aus verschiedenen Winkeln zeigen.
- Tangente: Eine tangentiale Ebene berührt eine Oberfläche an einem einzigen Punkt und steht senkrecht zur Linie, die durch diesen Punkt verläuft. Tangentialebenen sind in der Analysis und Differentialgeometrie wichtig, um die Beziehung zwischen Kurven und Flächen an einem bestimmten Punkt darzustellen.
- Parallel: Eine parallele Ebene schneidet sich nicht mit einer anderen Ebene und behält über ihre gesamte Länge den gleichen Abstand bei. Parallele Ebenen sind nützlich, um die Eigenschaften von Linien und Winkeln in Bezug auf parallele Flächen zu untersuchen.
- Senkrecht: Eine senkrechte Ebene bildet einen rechten Winkel (90 Grad) in Bezug auf eine andere Ebene oder Linie.
Unterschied zwischen Ebene und Fläche
In der Geometrie bezeichnet der Begriff "Ebene" eine zweidimensionale Fläche, die sich unendlich in alle Richtungen erstreckt, ähnlich wie ein Blatt Papier. Es ist eine abstrakte Entität ohne Dicke, definiert durch den Schnittpunkt zweier Linien oder durch Punktreihenfolgen im Raum.
Auf der anderen Seite ist "Fläche" eine quantitative Maßeinheit für die Ausdehnung einer zweidimensionalen Oberfläche. Sie repräsentiert die Menge an Raum, die von einer Figur auf der Ebene bedeckt wird, und wird in Quadrat-Einheiten (wie Quadratmeter oder Quadratzentimeter) ausgedrückt.
Während eine Ebene die Oberfläche selbst ist, ist die Fläche das numerische Maß dafür, wie viel Raum diese Oberfläche einnimmt.