Die Geometrie, einer der grundlegenden Zweige der Mathematik, ist für die Untersuchung von Formen, Größen, relativen Positionen geometrischer Objekte und den Eigenschaften des Raums verantwortlich. Eines der Schlüsselkonzepte dieser Disziplin ist die Winkelhalbierende.
Vereinfacht ausgedrückt ist eine Winkelhalbierende eine Linie, ein Strahl oder ein Segment, das etwas in zwei gleiche oder proportionale Teile teilt.
Der Begriff „Halbierende“ kommt vom lateinischen „bisectus“, was „in zwei Teile schneiden“ bedeutet. Die Winkelhalbierende wird in verschiedenen geometrischen Zusammenhängen verwendet, um Winkel, Segmente, Bögen und andere Elemente in gleiche oder proportionale Teile zu unterteilen.
Als nächstes werden wir untersuchen, wie die Winkelhalbierende in verschiedenen geometrischen Situationen angewendet wird.
Winkelhalbierende
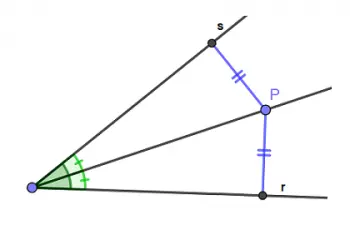
Eine der häufigsten Anwendungen der Winkelhalbierenden in der Geometrie ist die Winkelteilung. Die Winkelhalbierende ist eine Linie, die diesen Winkel in zwei kleinere Winkel mit demselben Maß teilt.
Mit anderen Worten: Teilen Sie den Winkel gemäß dem Winkelhalbierendensatz in zwei gleiche Teile. Dies ist nützlich zum Dreiteilen von Winkeln, zum Konstruieren spezifischer Winkel und zum Lösen geometrischer Probleme.
Die Winkelhalbierende kann man sich als Linie vorstellen, die am Scheitelpunkt des Winkels beginnt und ihn in zwei kongruente Winkel teilt.
Winkelhalbierende eines Segments
Die Winkelhalbierende kann auch auf Liniensegmente angewendet werden. Die Winkelhalbierende eines Segments teilt das Segment in zwei gleich lange Teile. Wenn wir ein Segment AB haben, teilt die Winkelhalbierende es in zwei Segmente AC und CB, wobei AC die gleiche Länge wie CB hat.
Diese Eigenschaft ist besonders nützlich, um den Mittelpunkt eines Segments zu ermitteln, was erhebliche Auswirkungen auf die analytische Geometrie und die Konstruktion äquidistanter geometrischer Figuren hat.
Winkelhalbierende eines Bogens
In der Kreisgeometrie ist eine Bogenhalbierende eine Linie, die den Bogen genau in zwei Hälften schneidet. Dies ist sehr nützlich bei Geometrieproblemen, bei denen eine präzise Teilung eines Kreises oder Bogens erforderlich ist.
Die Winkelhalbierende eines Bogens wird beispielsweise verwendet, um den Mittelpunkt eines Kreises zu bestimmen oder um einen Kreis in zwei gleich lange Bögen zu teilen. Dies ist wichtig für die Konstruktion kreisförmiger geometrischer Figuren und für die Lösung von Problemen im Zusammenhang mit Kreisen.
Winkelhalbierende in Dreiecken
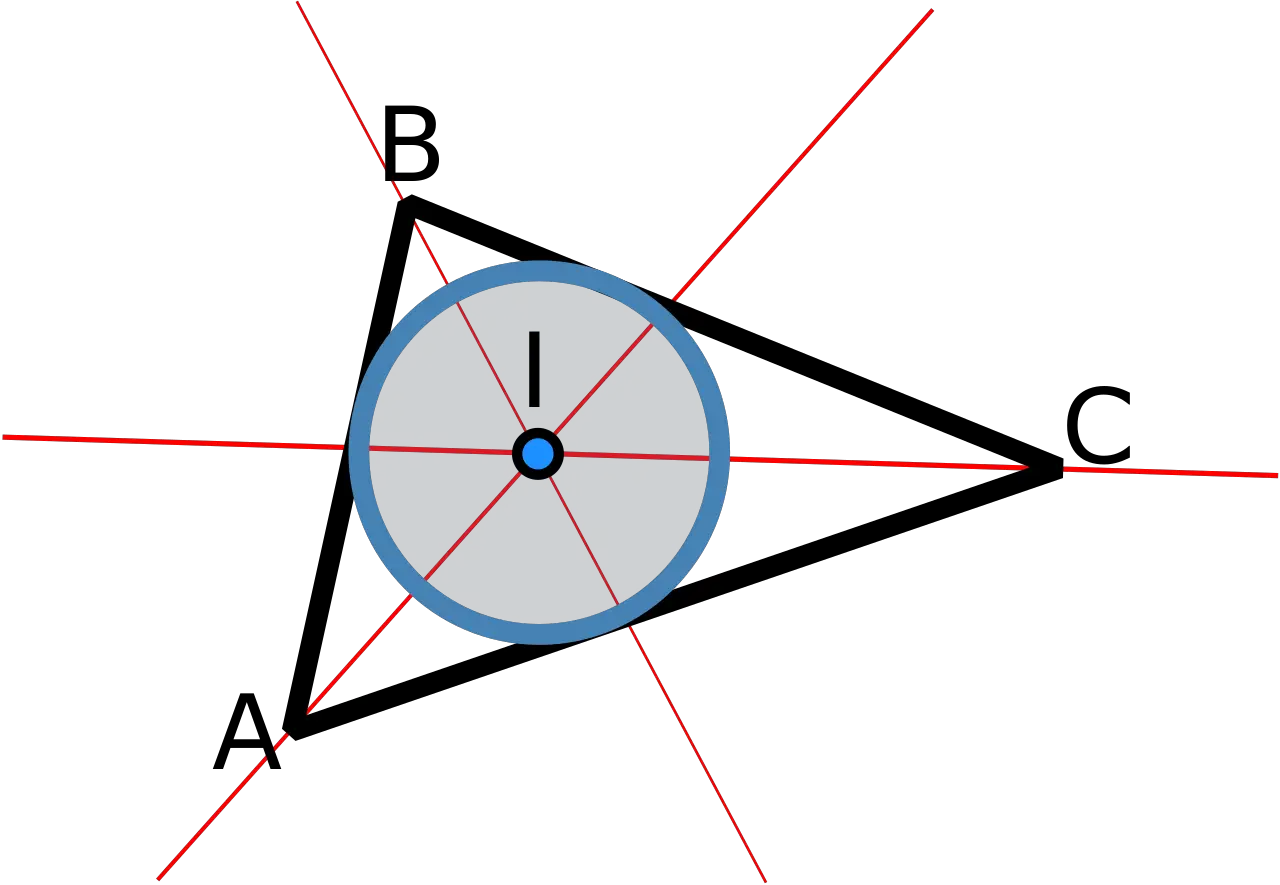Dieses Element spielt auch bei der Untersuchung von Dreiecken eine wichtige Rolle.
In einem Dreieck ist die Winkelhalbierende eine Linie, die am Scheitelpunkt des Winkels beginnt und die gegenüberliegende Seite in zwei Segmente teilt, die proportional zu den beiden anderen Seiten des Dreiecks sind. Dies ist als „Bisektorensatz“ bekannt und eignet sich zur Lösung trigonometrischer Probleme und zum Beweis der Eigenschaften von Dreiecken.
Der Satz besagt, dass das Verhältnis zwischen der Länge einer Seite des Dreiecks und der Länge des Segments, das die Winkelhalbierende auf dieser Seite bildet, gleich dem Verhältnis zwischen den beiden anderen Seiten des Dreiecks ist.
Diese Eigenschaft ist für die Lösung geometrischer Probleme mit Dreiecken und ihren Eigenschaften von großer Bedeutung.
Anwendungen der Winkelhalbierenden im Alltag
In der Architektur wird es beispielsweise zur Konstruktion präziser Winkel und proportionaler Unterteilungen in Gebäudeplänen und -entwürfen verwendet. Die Winkelhalbierende ermöglicht es Architekten und Designern, mühelos symmetrische und ausgewogene Strukturen zu schaffen.
In der Technik wird die Winkelhalbierende zur Bestimmung äquidistanter Punkte an Strukturen und Maschinen verwendet, was für die Gewährleistung von Stabilität und Präzision in verschiedenen Anwendungen unerlässlich ist.
Abschluss
Die Winkelhalbierende ist ein grundlegendes Konzept in der Geometrie, das zur Aufteilung von Winkeln, Segmenten, Bögen und anderen Elementen in gleiche oder proportionale Teile verwendet wird.
Seine Anwendung ist breit und vielseitig und spielt eine wesentliche Rolle bei der Lösung geometrischer Probleme, der Konstruktion geometrischer Figuren und der Demonstration mathematischer Eigenschaften. Das Verständnis der Winkelhalbierenden ist für diejenigen, die in die Welt der Geometrie und ihre Anwendung in verschiedenen Disziplinen einsteigen möchten, von wesentlicher Bedeutung.
Von der präzisen Winkelteilung in der Architektur bis zur Lösung trigonometrischer Probleme in der Mathematik ist die Winkelhalbierende ein leistungsstarkes Werkzeug, das eine herausragende Rolle bei der Lösung von Problemen und der Schaffung ausgewogener und symmetrischer Strukturen spielt.
