In der Geometrie stellen geometrische Körper eine wesentliche Kategorie dreidimensionaler Formen dar, die den Raum in drei Dimensionen einnehmen: Höhe, Breite und Länge. Diese durch Flächen, Kanten und Eckpunkte definierten Körper spielen eine grundlegende Rolle bei der Konzeptualisierung und dem Verständnis dreidimensionaler Strukturen.
Die Bedeutung dieser dreidimensionalen geometrischen Figuren liegt in ihrer Fähigkeit, reale und abstrakte Objekte im Raum zu beschreiben, was in Bereichen wie Architektur, Design und Ingenieurwesen von entscheidender Bedeutung ist.
Ein klassisches Beispiel ist der Würfel mit seinen sechs quadratischen Flächen und verbundenen Eckpunkten, der einen elementaren geometrischen Körper darstellt. Die Vielfalt geometrischer Körper, von der Pyramide bis zum Zylinder, ermöglicht es uns, den Formenreichtum der dreidimensionalen Welt, die uns umgibt, zu modellieren und zu verstehen.
Was ist ein geometrischer Körper?
Ein geometrischer Körper ist ein dreidimensionales Gebilde, das den Raum in den Dimensionen Höhe, Breite und Tiefe einnimmt. Diese dreidimensionalen Körper unterscheiden sich von zweidimensionalen Figuren und weisen Flächen, Kanten und Eckpunkte auf, die ihre Struktur definieren. Geometrische Körper umfassen verschiedene Formen, von Prismen und Pyramiden bis hin zu Kugeln und Zylindern, jede mit einzigartigen Eigenschaften.
Flache Flächen, scharfe Kanten und verbundene Eckpunkte tragen zur Charakterisierung dieser Festkörper im dreidimensionalen Raum bei.
Zusätzlich zu ihrer Bedeutung in Geometrie und Mathematik werden geometrische Körper in praktischen Anwendungen in Architektur, Design und Wissenschaft eingesetzt und dienen als wesentliche Werkzeuge für die Konzeptualisierung und Modellierung von Objekten in der dreidimensionalen Welt.
Polyeder: ein besonderer Fall
Polyeder sind ein Sonderfall geometrischer Körper, deren Flächen alle Polyeder sind. Unter ihnen können wir regelmäßige Polyeder und unregelmäßige Polyeder unterscheiden.
In der dreidimensionalen Geometrie entspricht ein Polyeder jedem Polygon in der zweidimensionalen Geometrie.
Regelmäßige Polyeder bestehen aus regelmäßigen Vielecken. Diese geometrischen Körper können nach der Anzahl der Flächen klassifiziert werden.
Regelmäßige Polyeder sind am symmetrischsten. Es gibt insgesamt neun reguläre Polyeder: fünf konvexe Polyeder und vier Sternpolyeder .
Ein konvexes Polyeder ist ein Polyeder, das einen konvexen Körper materialisiert, d. h. für jedes Punktpaar im Körper ist das lineare Segment, das sie verbindet, vollständig im Körper enthalten.
Die fünf konvexen Beispiele sind seit der Antike bekannt und werden platonische Polyeder genannt. Dies sind die dreieckige Pyramide oder Tetraeder, der Würfel, das Oktaeder, das Dodekaeder und das Ikosaeder.
Pyramidenstamm
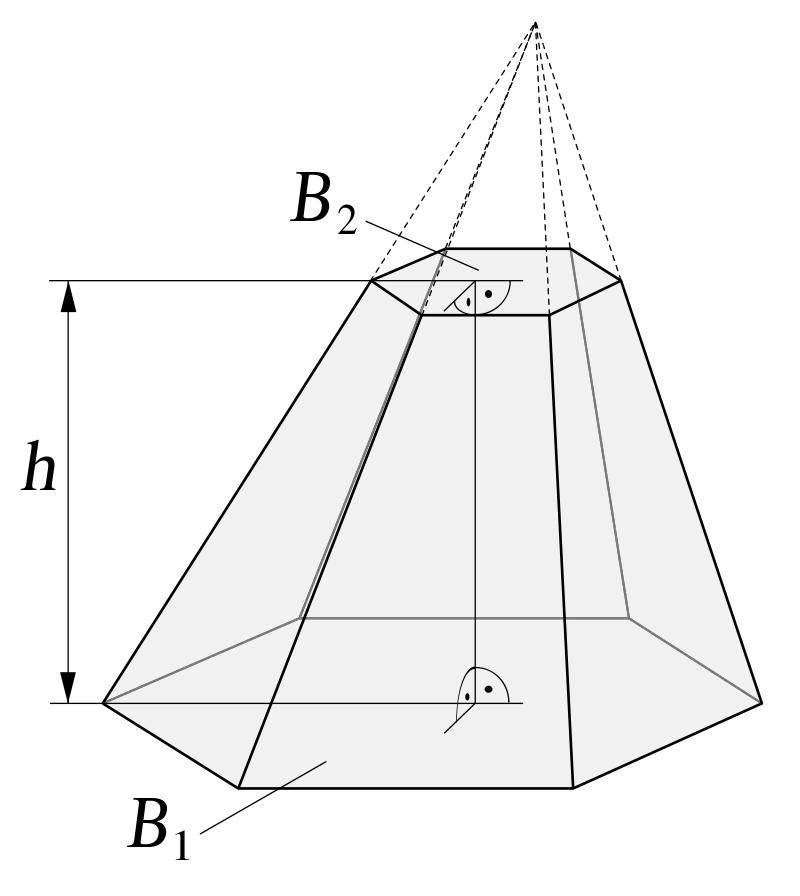Der Kegelstumpf einer Pyramide ist eine Art Polyeder, der aus zwei parallelen Grundflächen mit der gleichen Anzahl an Kanten besteht. Andererseits besteht es aus Seitenflächen in Form eines Trapezes. Die Anzahl der Flächen ist gleich der Anzahl der Kanten der Basen.
Dieses Polyeder erhält man, indem man eine Pyramide mit einer Zwischenebene parallel zu ihrer Basis schneidet. Von den beiden resultierenden Teilen ist der untere Teil ein Pyramidenstumpf und der obere Teil bleibt eine Pyramide.
Prismen
Ein Prisma ist ein Polyeder, zwei seiner Flächen sind gleich und liegen in parallelen Ebenen. Die übrigen Flächen des Prismas sind Parallelogramme, die mit diesen Polygonen gemeinsame Seiten haben. Diese Parallelogramme werden Seitenflächen des Prismas genannt, die beiden übrigen Polygone heißen Grundflächen.
Das an der Basis gefundene Polygon bestimmt den Namen des Prismas, zum Beispiel: Wenn die Basen Dreiecke sind, handelt es sich um ein dreieckiges Prisma.
Entsprechend der Basis kann das Prisma wie folgt benannt werden:
- Dreieckiges Prisma: Jede Basis hat die Form eines Dreiecks.
- Viereckiges Prisma: Jede der Basen hat die Form eines Vierecks.
- Fünfeckiges Prisma: Jede der Basen hat die Form eines Fünfecks.
- Sechseckiges Prisma: Jede Basis hat die Form eines Sechsecks.
- Achteckiges Prisma: Jede Basis hat die Form eines Achtecks.
Runde Körper
Wir definieren runde Körper als geometrische Körper, die mindestens eine gekrümmte Fläche haben. Diese Art von Körpern wird auch als Rotationskörper bezeichnet, da sie durch Drehen einer geometrischen Figur um eine Achse erhalten werden können.
Einige Beispiele für runde Körper sind:
- Die Kugel ist die Figur, die durch die Drehung eines Kreises um eine Achse entsteht, die durch den Mittelpunkt verläuft. In diesem Fall hat es eine einzige gekrümmte Oberfläche und keine Kanten. Darüber hinaus haben alle Punkte auf der Oberfläche den gleichen Abstand vom Mittelpunkt der Kugel.
- Der Kegel entsteht, indem man ein rechtwinkliges Dreieck um eines seiner Beine dreht. Diese Figur hat ein einzelnes flaches Gesicht, das von einem Kreis gebildet wird.
- Der Zylinder entsteht durch Drehen eines Rechtecks um eine seiner Seiten.
Alltagsbeispiele
- Fußball : Der Fußball zeigt die Perfektion einer Kugel und veranschaulicht die häufige Präsenz dieser geometrischen Form in Alltagsgegenständen.
- Planeten des Sonnensystems : Die Himmelskörper des Sonnensystems nehmen kugelförmige Formen an, was die Vorherrschaft der Kugel in der Konfiguration des Universums unterstreicht.
- Karton : Mit seiner Struktur, die der Form eines rechteckigen Prismas, einem sogenannten Quader, folgt, sind Kartons greifbare Beispiele für geometrische Figuren in gängigen Verpackungen.
- Pyramiden von Ägypten : Die Pyramiden repräsentieren architektonische Majestät und sind Beispiele für viereckige Pyramiden, die den Test der Zeit bestanden haben.
Diese Beispiele verdeutlichen, wie untrennbar die Geometrie in unserer Umgebung vorhanden ist, von Alltagsgegenständen bis hin zu historischen Denkmälern.